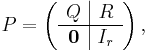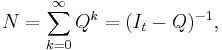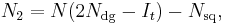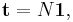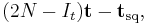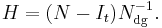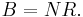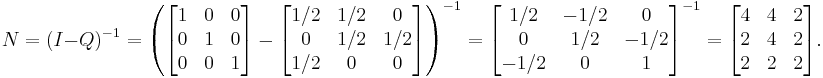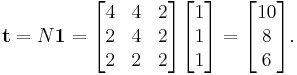Absorbing Markov chain

In the mathematical theory of probability, an absorbing Markov chain is a Markov chain in which every state can reach an absorbing state. An absorbing state is a state that, once entered, cannot be left.

Like general Markov chains, there can be continuous-time absorbing Markov chains with an infinite state space. However, this article concentrates on the discrete-time discrete-state-space case.

Contents

Formal definition

A Markov chain is an absorbing chain if

  1. there is at least one absorbing state and
  2. it is possible to go from any state to at least one absorbing state in at a finite number of steps.

In an absorbing Markov chain, a state that is not absorbing is called transient.

Canonical form

Let an absorbing Markov chain with transition matrix P have t transient states and r absorbing states. Then

P = \left( \begin{array}{c|c} Q & R\\ \hline \mathbf{0} & I_r \end{array} \right),

where Q is a t-by-t matrix, R is a nonzero t-by-r matrix, 0 is an r-by-t zero matrix, and Ir is the r-by-r identity matrix. Thus, Q describes the probability of transitioning from some transient state to another while R describes the probability of transitioning from some transient state to some absorbing state.

Fundamental matrix

A basic property about an absorbing Markov chain is the expected number of visits to a transient state j starting from a transient state i (before being absorbed). The probability of transitioning from i to j in exactly k steps is the (i,j)-entry of Qk. Summing this for all k (from 0 to ∞) yields the desired matrix, called the fundamental matrix and denoted by N. It is easy to prove that

N = \sum_{k=0}^\infty Q^k = (I_t - Q)^{-1},

where It is the t-by-t identity matrix. With the matrix N in hand, other properties of the Markov chain are easy to obtain.[2]

Variance on number of visits

The variance on the number of visits to a transient state j with starting at a transient state i (before being absorbed) is the (i,j)-entry of the matrix

N_2 = N (2 N_{\operatorname{dg}} - I_t) - N_{\operatorname{sq}},

where Ndg is the diagonal matrix with the same diagonal as N and Nsq is the Hadamard product of N with itself (i.e. each entry of N is squared).

Expected number of steps

The expected number of steps before being absorbed when starting in transient state i is the ith entry of the vector

\mathbf{t} = N \mathbf{1},

where 1 is a length-t column vector whose entries are all 1.

Variance on number of steps

The variance on the number of steps before being absorbed when starting in transient state i is the ith entry of the vector

(2 N - I_t) \mathbf{t} - \mathbf{t}_{\operatorname{sq}},

where tsq is the dot product of t with itself (i.e. each entry of t is squared).

Transient probabilities

The probability of visiting transient state j when starting at a transient state i is the (i,j)-entry of the matrix

H = (N - I_t) N_{\operatorname{dg}}^{-1}.

Absorbing probabilities

Another property is the probability of being absorbed in the absorbing state j when starting from transient state i, which is the (i,j)-entry of the matrix

B = N R.

Examples

String generation

Main article: String generation

Consider the process of repeatedly flipping a fair coin until the sequence (heads, tails, heads) appears. This process is modeled by an absorbing Markov chain with transition matrix

P = \begin{bmatrix} 1/2 & 1/2 & 0 & 0\\ 0 & 1/2 & 1/2 & 0\\ 1/2 & 0 & 0 & 1/2\\ 0 & 0 & 0 & 1 \end{bmatrix}.

The first state represents the empty string, the second state the string "H", the third state the string "HT", and the fourth state the string "HTH". Although, the coin flips cease after the string "HTH" is generated, the perspective the absorbing Markov chain is that the process has transitioned into the absorbing state representing the string "HTH" and, therefore, cannot leave.

For this absorbing Markov chain, the fundamental matrix is

N = (I - Q)^{-1} = \left( \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} - \begin{bmatrix} 1/2 & 1/2 & 0\\ 0 & 1/2 & 1/2\\ 1/2 & 0 & 0 \end{bmatrix} \right)^{-1} = \begin{bmatrix} 1/2 & -1/2 & 0\\ 0 & 1/2 & -1/2\\ -1/2 & 0 & 1 \end{bmatrix}^{-1} = \begin{bmatrix} 4 & 4 & 2\\ 2 & 4 & 2\\ 2 & 2 & 2 \end{bmatrix}.

The expected number of steps starting from each of the transient states is

\mathbf{t} = N \mathbf{1} = \begin{bmatrix} 4 & 4 & 2\\ 2 & 4 & 2\\ 2 & 2 & 2 \end{bmatrix} \begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix} = \begin{bmatrix} 10\\ 8\\ 6 \end{bmatrix}.

Therefore, the expected number of coin flips before observing the sequence (heads, tails, heads) is 10, the entry for the state representing the empty string.

Games of chance

Games base entirely on chance can be modeled by an absorbing Markov chain. A classic example of this is the ancient Indian board game Snakes and Ladders. The graph on the right[3] plots the probability mass in the lone absorbing state that represents the final square as the transition matrix is raised to larger and larger powers. To determine the expected number of turns to complete the game, compute the vector t as described above and examine tstart, which is approximately 39.2.

See also

References

  1. ^ Grinstead, Charles M.; Snell, J. Laurie (July 1997). "Ch. 11: Markov Chains". Introduction to Probability. American Mathematical Society. ISBN 978-0821807491. http://www.cs.virginia.edu/~gfx/Courses/2006/DataDriven/bib/texsyn/Chapter11.pdf. 
  2. ^ Kemeny, John G.; Snell, J. Laurie (July 1976) [1960]. "Ch. 3: Absorbing Markov Chains". In Gehring, F. W.; Halmos, P. R.. Finite Markov Chains (Second ed.). New York Berlin Heidelberg Tokyo: Springer-Verlag. pp. 224. ISBN 978-0387901923. 
  3. ^ Based on the definition found in S. C. Althoen, L. King, K. Schilling (March 1993). "How Long Is a Game of Snakes and Ladders?". The Mathematical Gazette (The Mathematical Gazette, Vol. 77, No. 478) 78 (478): 71–76. doi:10.2307/3619261. JSTOR 3619261. 

External links